Symbolic computing and deep learning tutorial with Tensorflow / Theano : learn basic commands of 2 libraries for the price of 1
I gave a short presentation about Google Tensorflow previously, with install instructions. For Theano, it is as simple as a pip install theano.
Let’s put things in order to have a great tutorial with mixed code and explanations and learn twice faster with mixed Theano and Tensorflow examples in one tutorial :) You’ll discover how close the two libraries are. You can also use this tutorial to make your choice between the two libraries.
First launch a iPython session and import the two libraries. For Tensorflow, we have to create a session to run the operations in :
# tensorflow
import tensorflow as tf
sess = tf.Session()
# theano
import theano
import theano.tensor as th
Instructions beginning with tf will be Tensorflow code, with th Theano code.
Symbols in symbolic computing
Symbolic computation is a very different way of programming.
Classical programming defines variables that hold values, and operations to modify their values.
In symbolic programming, it’s more about building a graph of operations, that will be compiled later for execution. Such an architecture enables the code to be compiled and executed indifferently on CPU or GPU for example. Symbols are an abstraction that does not require to know where it will be executed.
The second aspect of symbolic computing is that it is much more like mathematical functions or formulas, that can be added, multiplied, differentiated, … to give other math functions. For example let’s define an addition :
# tensorflow
a = tf.placeholder(tf.int8)
b = tf.placeholder(tf.int8)
sess.run(a+b, feed_dict={a: 10, b: 32})
# theano
a = th.iscalar()
b = th.iscalar()
f = theano.function([a, b], a + b)
f(10,32)
a and b are not classical programming variables, but symbols or placeholders or tensors or symbolic variables. They are much more like mathematical variables. The second advantage of symbolic computing is the automatic differentiation, useful to compute gradients. For example let’s differentiate the function \(x \rightarrow x^2\) in Theano :
# theano
a = th.dscalar()
ga = th.grad(a ** 2,a)
f = theano.function([a], ga)
f(2)
This is great since it does not require to know how to differentiate a function. As you can see, both in Theano and Tensorflow, the z = a + b is of type Tensor as a and b.
Tensors are not variables and have no value, but can be evaluated which will launch the operations in a session run as before or directly written :
# theano
z = a + b
print z.eval({a : 10, b : 32})
# tensorflow
z = a + b
with sess.as_default():
print z.eval({a: 10, b: 32})
# or z.eval(feed_dict={a: 10, b: 32})
Tensors have a type and a shape as in Numpy (their full specification : Tensorflow types and shapes - Theano types).
Naming tensors in the graph of operations
Tensorboard, part of Tensorflow, offers us to follow the graph construction state, which is a good idea in parallel of this tutorial. Let’s first write the definition of the graph to the log file :
# tensorflow
writer = tf.train.SummaryWriter("/tmp/mytutorial_logs", sess.graph_def)
writer.flush()
and launch Tensorboard :
tensorboard --logdir=/tmp/mytutorial_logs
Go to http://localhost:6006/ and under the graph tab to see the first graph :
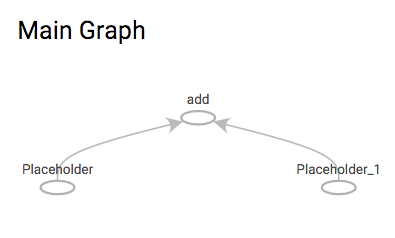
As you can see, our addition operation is present but symbols are not named, it is possible to name them for debugging or display in Tensorboard :
# tensorflow
a = tf.placeholder(tf.int8, name="a")
b = tf.placeholder(tf.int8, name="b")
addition = tf.add(a, b, name="addition")
sess.run(addition, feed_dict={a: 10, b: 32})
# theano
a = th.iscalar('a')
b = th.iscalar('b')
f = theano.function([a, b], a + b, name='addition')
f(10,32)
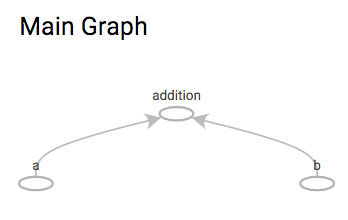
Tensorflow offers namescopes that add a scope prefix to all tensors declared inside the scope, and Tensorboard displays them under a single node that can be expanded in the interface by clicking on it. Scopes can be hierarchical also.
# tensorflow for tensorboard
a = tf.placeholder(tf.int8, name="a")
b = tf.placeholder(tf.int8, name="b")
with tf.name_scope("addition") as scope:
my_addition = a+b
sess.run(my_addition, feed_dict={a: 10, b: 32})
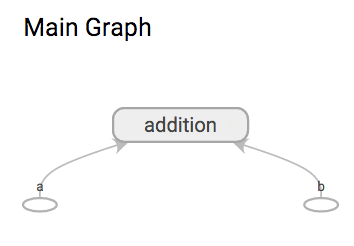
Share the variables in a first example of network
Let’s go a bit further and define in symbolic computing (as I did in my Caffe tutorial) a first layer of 3 neurons acting on MNIST images (size 28x28=784, 1 channel) with zero padding, stride 1 and weights initialized with a normal distribution.

In symbolic computation, tensors are abstraction objects of the operations and objets in the memory of the CPU or the GPU, simplifying manipulation, but how can we access their values outside from the result values of a session run ?
For that purpose, Tensorflow created Variables, that add an operation to the graph, are initiated with a tensor and have to be initialized before the run (None in the shape definition defines any size for this dimension) :
# tensorflow
x = tf.placeholder(tf.float32, [None, 784])
weights = tf.Variable(tf.random_normal([5, 5, 1, 3], stddev=0.1))
bias = tf.Variable(tf.constant(0.1, shape=[1,3]))
x_image = tf.reshape(x, [-1,28,28,1])
z = tf.nn.conv2d(x_image, weights, strides=[1, 1, 1, 1], padding='SAME') + bias
sess.run(tf.initialize_all_variables())
and Theano shared variables, initialized with Numpy arrays :
# theano
import numpy as np
from theano.tensor.nnet import conv
x = th.tensor4(name='input', dtype='float64')
weights = theano.shared( 0.1 * np.random.randn(5,5,1,3), name ='weights')
bias = theano.shared( np.asarray([0.1,0.1,0.1], dtype='float64'), name ='bias')
output = conv.conv2d(x, weights) + bias
f = theano.function([x], output)
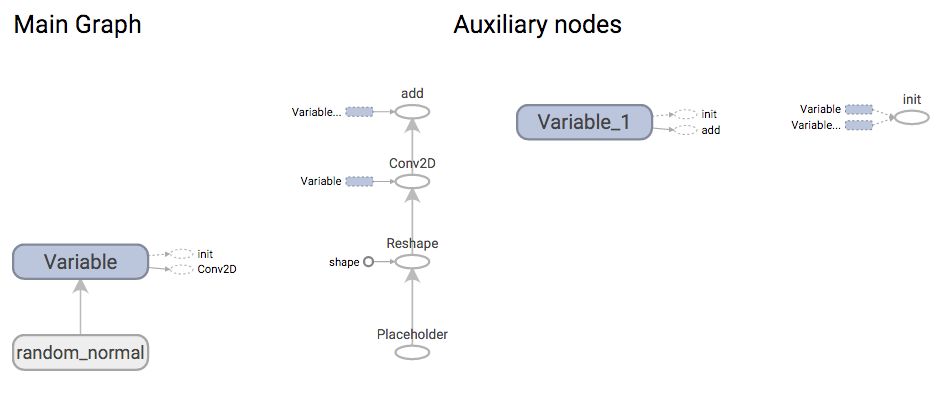
Conclusion
With this simple introduction to symbolic programming, you’re now ready to go further and check out Tensorflow net examples and Theano net examples !
A very nice library that is built on top of Theano and simplifies the use of Theano is Lasagne.
Concepts such as tensors are very close to the Numpy arrays or BIDMach matrices, a very nice CPU/GPU abstraction for Scala.
Spark programming is also symbolic, with a graph of operations that will be compiled and executed in a session on the cluster of instances when an output is demanded.
I’m eager to see the next symbolic library that will go one step further, combining the graph of CPU/GPU computing as Tensorflow/Theano/BIDMach do, and the graph of cluster computing as Spark does, into one single graph that can be executed anywhere, on a CPU, a GPU, or a cluster of instances indifferently.
Hopefully you enjoyed !