1-grid LSTM and the XOR problem
A short post about a very nice classifier, the 1-Grid-LSTM, and its application to the XOR problem, as proposed by Nal Kalchbrenner, Ivo Danihelka, Alex Graves in their paper.
The XOR problem consists in predicting the parity of a string of bits, 0 and 1. If the sum of the bits is odd, the target is the 0. If the sum of the bits is even, the target is 1.
The problem is pathological in the sense a simple bit in the input sequence can change the target to its contrary. During training, accuracy is not better than random for a while, although a kind of engagement can be observed in a wavy growth of the accuracy to 100%.
Building a network manually, or building a recurrent network with the bits as input sequence to the RNN, are easy. The latter is a simple 2-bit parity problem.
The k-bit parity problem, for high values of k, is a much more complicated problem for a feed forward network training via gradient descent on full bit strings as input. The 1-Grid LSTM is a feed forward network that solves this problem very nicely, demonstrating the power of the grid.
The story
Grid LSTM have been invented in continuity of stacked LSTM and multi-dimensional LSTM. They present a more general concept, much precise than stacked LSTM and more stable than multi-dimensional LSTM.
Since it is complicated to visualize a N-Grid LSTM let’s consider the case in 2D : the 2-Grid-LSTM.
The 2-Grid-LSTM is composed of 2 LSTM running on 2 different dimensions (x,y), given by the following equation :
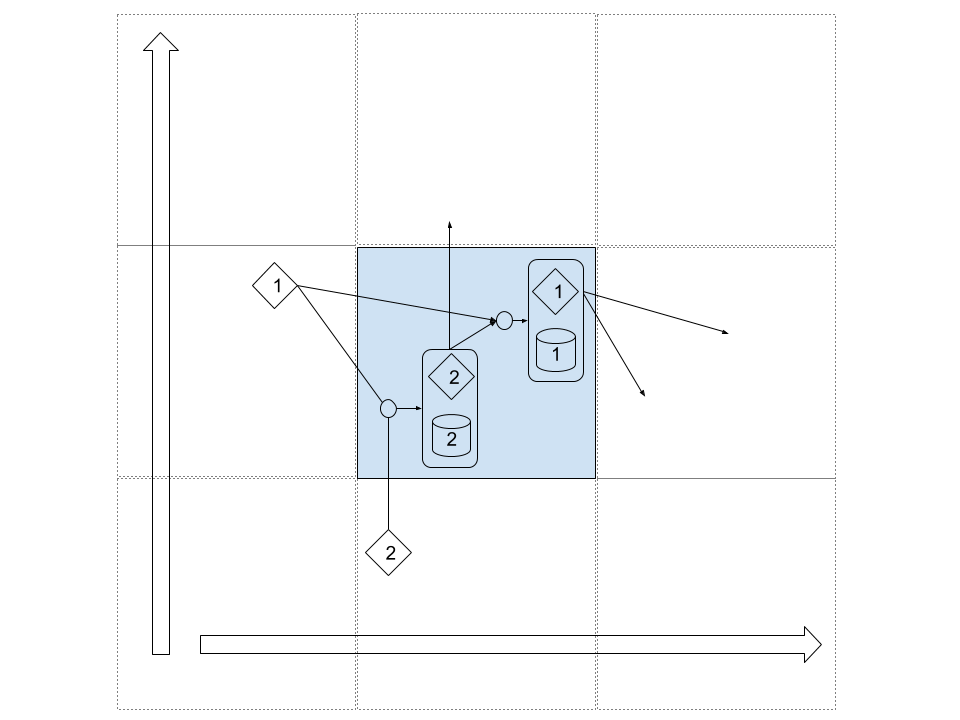
\[h_2^{x,y}, m_2^{x,y} = \text{LSTM}_2 (h_1^{x,y-1}, h_2^{x,y-1}, m_2^{x,y-1})\] \[h_1^{x,y}, m_1^{x,y} = \text{LSTM}_1 (h_1^{x-1,y}, h_2^{x,y}, m_1^{x-1,y})\]To get a good idea of what it means, you can consider a 2-Grid-LSTM as a virtual cell traveling on a 2 dimensional grid :
LSTM 1 uses the hidden state value of the LSTM 2, in this case \(h_2^{x,y}\), instead of its previous value. This helps the network learn faster correlation between the two LSTM. There is always a notion of priority and order in the computation of the LSTM. Parallelisation of the computations require to take this into consideration.
For each cell in the grid, there can be an input and/or an output, as well as no input and/or no output.
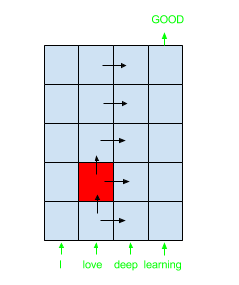
In the case of 1D sequences (times series, textes, …) for which 2-GRID LSTM perform better than stacked LSTM, input is given for the bottom row, as shown with the input sentence “I love deep learning” in the above figure.
In case of text classification, output will be given for the last cell top right (as shown with “Good” output label in the above figure).
The first dimension is usually the time (x), the second dimension the depth (y).
A drawing of the mecanism and the connections inside the cell would be :
1-Grid LSTM, a special case
The 1-Grid LSTM is a special case since the LSTM is used along the depth dimension to create a feedforward classifier instead of a recurrent network. It looks as follow :
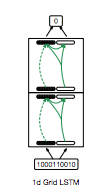
It looks very closely to a LSTM, but with the following differences :
-
there is no input at each step in the recurrence of the LSTM, and the recurrence is used along the depth dimension as a gated mecanism (such as in a Highway networks)
-
the input is fed into the hidden state and cell state instead, thanks to a linear projection
The XOR problem shows the power of such network as classifiers. Here are two implementations, one in Theano, another in Torch :
1-Grid-LSTM is very close to memory networks, networks that are also recurrent along the depth dimension, but whose weights can vary depending on a memory that is being feed with statements or facts.
Recurrency along the depth sounds to me very close to natural reasoning, for which I have the feeling our brain is spinning for a certain amount of time, until it founds the solution. But that is not very scientific…
Recurrent Highway Networks also use this kind of recurrency.
Generalization
The N-Grid LSTM is a improvement of the multi-dimensional LSTM.
The option to untie the weigths in the depth direction is considered also during evaluation of models. To be precise two options are possible :
-
the LSTM 1 at different level y can have different weigths. It is usually the case in many implementations.
-
the LSTM 2 can be transformed into a feedforward model, where weights are not shared between the different level y. In this case, it is also possible to remove the cell in the LSTM 2 and replace the LSTM mecanism by a non-linearity, to come back to the stacked LSTM architecture.
In this sense, N-Grid-LSTM with the option of untying the weights and modifying the mecanism along the depth dimension, is a generalization of stacked LSTM.
Nice!